Bei Tangram fallen uns laufende oder teetrinkende Männchen ein, die es nachzulegen gilt. Nur wenige wissen, dass das Legespiel auch im Geometrieunterricht erfolgreich zum Einsatz kommt. In diesem Blog erfahren sie, wie.
Doch Tangram ist nicht nur ein kurzweiliger Rätselspaß, sondern es steckt auch jede Menge Geometrie darin.
Das Legespiel besteht aus sieben verschiedenen Polygonen (Vielecken), die sich zu einem Quadrat zusammenlegen lassen. Es sind fünf Dreiecke, ein Quadrat und ein Parallelogramm. Für eine Tangram-Figur müssen alle sieben Teile verwendet werden, die Teile müssen sich berühren, dürfen sich aber nicht überdecken.
Folgende Lerninhalte können mit Tangram im Geometrieunterricht vermittelt werden:
- Geometrische Flächen werden vertraut gemacht
- Das Augenmaß wird im Vergleichen von Formen trainiert
- Logik und Kreativität werden gleichermaßen gefördert
- Räumliches Vorstellungsvermögen wird geschärft
- Kongruente Linien und Flächen werden identifiziert
1. Übung: Das Raster
Lassen sie doch zu Beginn der Arbeit mit dem Tangram ihre Schüler*innen das Tangram zerlegen und wieder zu einem Quadrat zusammensetzen. Vielleicht sind sie erstaunt, wie schwierig das ist, obwohl das Quadrat ja noch kurz vorher vor ihnen lag.
Generell gilt beim Tangram: Je einfacher die äußere Form, desto schwieriger die Lösung.
Über das Tangram in seiner Ausgangsform lässt sich ein Raster aus 16 Quadraten legen. Dessen Eckpunkte fallen genau mit allen Eckpunkten der Tangramteile zusammen. Da die Kanten der Tangramteile immer auf den vertikalen, horizontalen oder diagonalen Linien des Rasters liegen, wird deutlich, wie viele Seiten der Tangramteile exakt dieselbe Länge besitzen. Dadurch gibt es fast unzählige Möglichkeiten, die einzelnen Teile zu geometrischen Figuren zu verbauen.
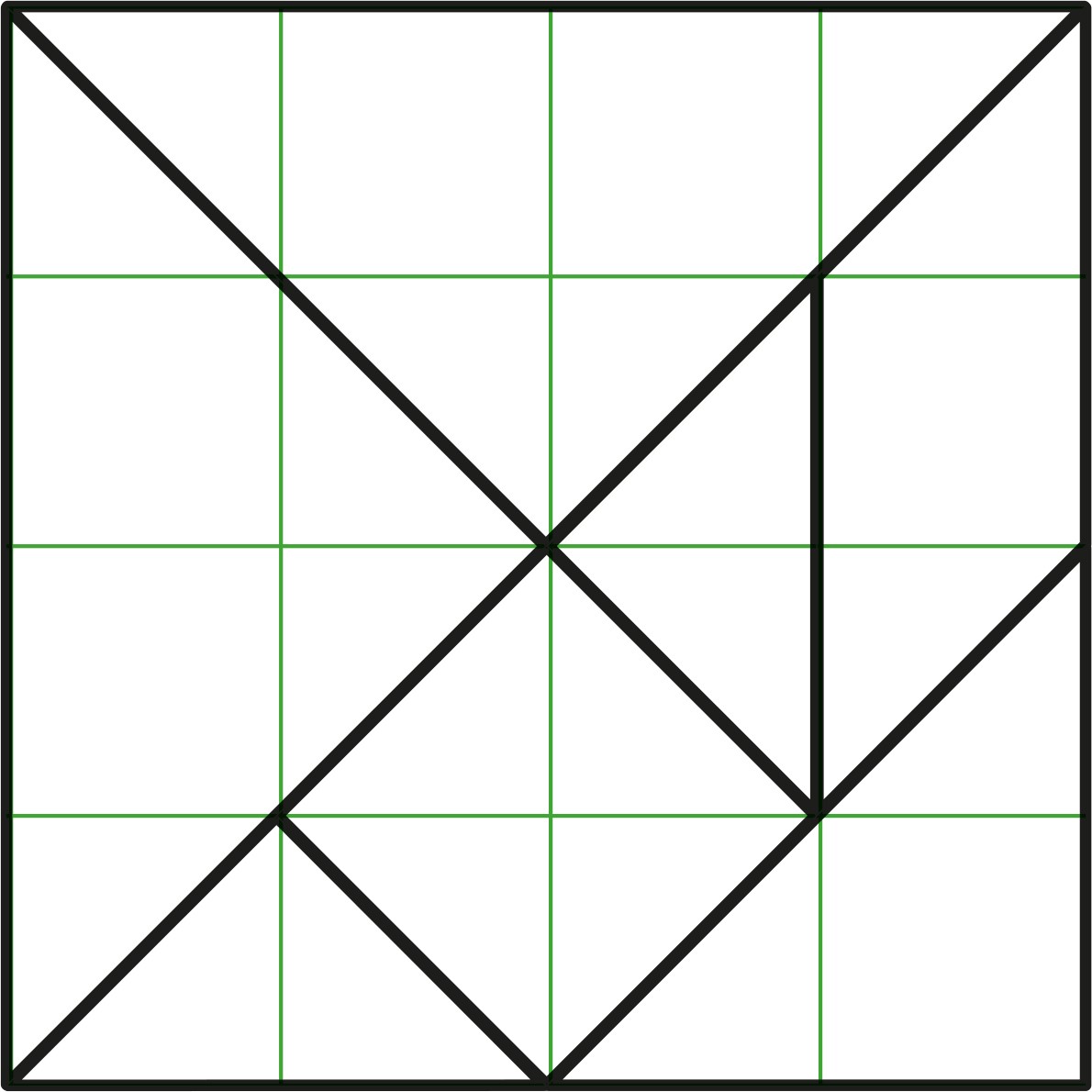
Die Schüler*innen haben das Große Tangram-Quadrat vor sich liegen und messen die Umrisse genau ab. Dann zeichnen sie das Quadrat mit Hilfe von Lineal und Geodreieck auf Transparentpapier genau ab und zeichnen auch die einzelnen Tangramteile ein. Nun teilen sie das gezeichnete Quadrat in 16 Unter-Quadrate und zeichnen auch diese ein.
Lassen sie nun ihre Schüler*innen die einzelnen Tangramflächen berechnen.
Welche Entsprechungen gibt es? (z.B. kleines Quadrat und Raute)
Etwa die Berechnung Großes Dreieck: A = ½ x g · h = ½ x 4 x 2 = 4
Die Schüler*innen können ihre Ergebnisse leicht anhand des Rasters überprüfen:
Großes Dreieck: A = 2 ganze Quadrate + 4 x ½ Quadrat = 4 Quadrate. Dank des Rasters lässt sich auch ohne Rechnen die Größe der einzelnen Flächen erkennen.
Weitere Übungen:
- Die Schüler*innen versuchen, eine vorgegebene Form nachzulegen. Geometrisch oder figural.
In unserem Tangram-Heftchen finden sie 40 verschiedene Figuren mit Lösungen:
2. Wie viele Zwillinge, also identische Figuren lassen sich legen? Jedes Zwillingspaar wird aus den 7 Tangramformen gelegt.
3. Kreative Schüler*innen haben sicherlich Freude daran, eigene Figuren zu entwickeln. Menschliche und tierische sind dabei besonders beliebt.
4. Auch das Tangram selbst kann neu gestaltet werden. Quadratisch, rechteckig, rund oder herzförmig. Die Teile können
aus Karton ausgeschnitten oder aus Holz gesägt werden.
5. Attraktiv für den Unterricht ist auch das große magnetische Tangram:
6. Eine allgemeine Einführung in die Welt des Tangrams (Seite nach unten scrollen) und verschiedene Ausführungen finden
sie hier:
Bildernachweis: Shutterstock/tomertu/marekuliasz Autorin: Marie Laschitz



